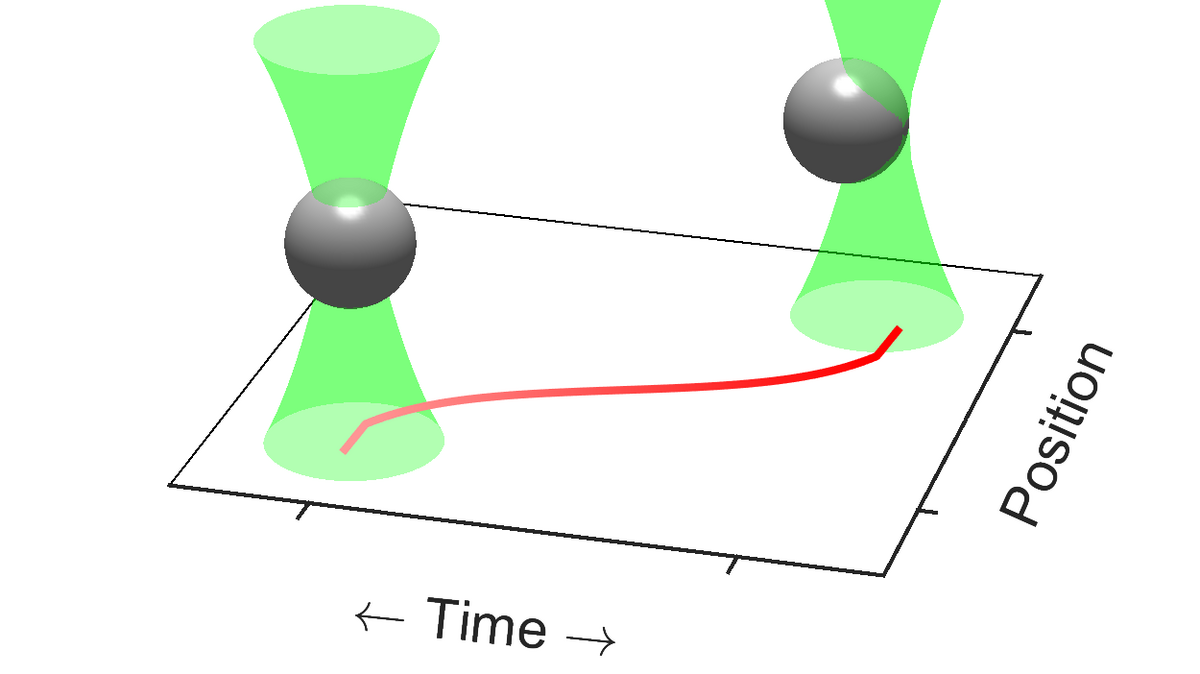
Optimal control

Optimizing the energy efficiency of driving processes provides valuable insights into their underlying  physics and is of crucial importance for numerous applications, from biological processes to the design of machines and robots.

We consider experimentally and theoretically a  paradigmatic optimization problem at the microscale, namely the motion of a harmonic potential carrying a load through a surrounding fluid, in  a finite time and over a given distance, using as little work as possible. In contrast to previous studies, we take into account memory effects in the surrounding fluid due to internal relaxation processes, which are ubiquitous in real-world applications, e.g., play a central role in subcellular transport. Using optical trapping experiments with a colloidal particle in a viscoelastic and a purely viscous fluid, we show that such memory effects significantly alter the optimal driving strategies, in agreement with our analytical predictions using variational calculus. Surprisingly, we find that regardless of the form of the memory kernel or the noise properties, the mean particle trajectory and the transport protocol always obey time-reversal symmetry, as long as the dynamics can be treated in its linear regime. We present a rigorous theoretical proof that such symmetry, which is usually a hallmark of thermal equilibrium, is a fundamental property of optimal driving processes in a variety of systems, thus serving as a robust and versatile tool for detecting optimal protocols. Using a machine learning algorithm, we demonstrate that the algorithmic exploitation of time-reversal symmetry can significantly reduce the computation time of optimization problems.